Our school is doing remote learning, like every school I know whose year hasn’t ended. With the end of this year comes urge to move past hastily planned system we have been running since March, and look forward to the fall. Most people are postponing thinking about the fall because every time the mayor or governor holds a press conference they can’t say what the fall will be. The truth is, we already have all the information we need to start planning, and the first step is in looking real hard at this remote situation that many of us our mired in.  Uncertainty about next school year will loom from now until it September, and will be a constant through June. Luckily, the design of this web page can help to provide a clear idea of how to plan around uncertainty.

Web Page Designs Drastic Shift

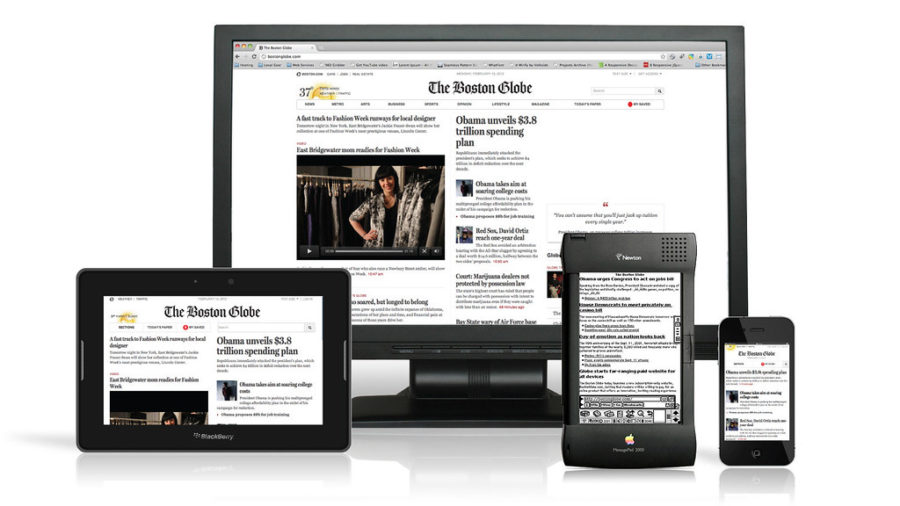
For the last decade, web designers have struggled to build websites that deliver content and look beautiful, despite companies constantly creating new devices to view the site to on.  Modern websites instantaneously adapt to screen sizes as wide as a smartboard and as skinny as a smartphone. To see this in action, try experimenting with the size of this window. As you decrease the width of your browser window, the image of the 4 devices at the top stays perfectly sized for your window. Shrink it enough and you’ll notice menu icons appear. When it’s as small as the width of a smartphone screen, title of my site snuggles down next to the menu icons, conserving screen real estate, the font is easier to read, while the image at the the top still fits in the window. Websites didn’t always do this.

Comparing the ESPN website from 2010 and 2020 shows that actively adapting websites weren’t always around. Advances in technology created a litany of web-ready devices, so website developers had to build the  adjustments to the big screen, the small screen, and every screen in between. Having a website solely for a full-screen computer was as typical for ESPN and other companies as the 7-period school day is for NYC educators. The consistency and predictability of web design was unmoored by Apple’s 2010 invention iPad, as neither the desktop or iphone sized sites really good on the really popular device. How they addressed the needs in these website issues maybe have some valuable lessons for schools looking to address the litany of fears surrounding this pandemic.

Adapt Respond Overcome

After COVID-19 forced a blunt introduction to remote learning this spring, schools now can expect a fall where being able to slide into remote learning is a new normal. Schools will be expected to dust off the Google Classroom and Flipgrid if next year brings a second wave, or some families decide to stay in quarantine, or an outbreak happens in school. This experiment has been difficult and unfamiliar, but likely to return in the fall if the pandemic is still going. How can you map out any calendar for the year if your school will still be in the building, remote, or doing some kind of hybrid? With vaccine deployment expected in second semester at it’s most optimistic, your school can expect to snap in to a significant portion of time. It would be nice if we could switch between the old  model and this new remote thing, flexibly, right? Almost as flexibly as a … Reposnsive website?

Responsive Web Design was born a few months after the iPad in an influential blog post by Ethan Marcotte. In that post he provided an example of a responsive website that now looks standard, but was like a Back 2 The Future Guitar Solo at the time. He writes:

This is our way forward. Rather than tailoring disconnected designs to each of an ever-increasing number of web devices, we can treat them as facets of the same experience.

Wouldn’t it be great if next year could feel like one coherent experience? The news of a positive test hits your school community, in mid-October, not only does your school know how to shift the learning, but the clubs, events, and all other parts of the school experience know how to shift as well. Following some of the ideas of the web design, we could try to create a responsive school experience, in the hopes of ensuring for more equitable education in the face of these challenges.

Remote First

The first step for planning for next year should be to think through a remote learning approach that fits your values. Returning to remote learning in the fall is as appetizing as returning to that nightmare I had where I was surrounded by pirahnas. However if a second wave is remotely probably for the fall, returning to it with a plan you feel good about would be like returning to the pirahana dream, but with live preservers, or better yet a boat. Tightening up this step might involve the following:

• Reflect – How was this spring? What headaches were caused for teachers, students, parents and staff? What worked? What things were absent in a way that made you sad? For those of us (still) working in June, you may want to send out surveys, and collect artifacts to enhance your reflection.
• Tighten – Figure out ways to make the remote learning better.
• Extend – Make a plan for a whole year of remote, not just something that could work for a couple of months. Make the ship, not the lifeboat.

Planning “Remote First” is key because it has the most restrictions. The phrase “Mobile First” has been the ethos at Google since 2010 because after tackling the challenging restrictions of mobile computing there is also great opportunity for the future. Once these most challenging problems have been tackled, it is now possible to build more amazing experiences everywhere else.

These are some big remote learning questions (that I wish I had answer to, and would appreciate thoughts in the comments)?

• How do you have useful discussions?
• How can students meaningfully collaborate?
• How do you build community?
• How do you support students with special needs in all of the above?
• How can you monitor student work?

With the remote plan figured out, it is now possible to go to the opposite end and think through the completely optimistic full-year building plan. It’s not quite as simple as taking what was supposed to happen this year, since the building plan needs to avoid contradicting the remote plan. If the remote plan is using some app to build community, use it the building too. If the remote plan can’t include that super awesome hand-on project, don’t include it here. Better yet, figure out how to do remotely, update the remote plan but add the full-glory version to the building plan. Having the two plans mapped out should eventually look like two trains running on parallel tracks. This is key since there is probably going to be some jumping back and forth between trains through the year. Starting with the constraining remote plan first will ensure a coherent experience for people no matter which train they are on. Deciding when to jump trains is the reason from breakpoints.

Breakpoints

Website designers use breakpoints to define where a website needs to change for given the size of a users window. For example, if the width  of this window gets smaller than than 1000px the sidebar disappears. If it gets lower than 784 the navigation changes. The breakpoints continue until at 500px the full mobile layout takes over.  These breakpoints are aligned where the major device screen sizes would be and the designer made sure to plan which elements of the mobile layout and the desktop layout would be the right amount at each breakpoint.

A Breakpoint for a school might be an hybrid where some people are remote, others are in the building. For example, one positive test result could send a whole group of students into self quarantine. A breakpoint here would be helpful think through. These students’ teachers would know to move their instruction to the remote train, and in thinking through this breakpoint, maybe some letters home were drafted to communicate this to parents. A similar breakpoint could involve teachers being out on quarantine in such number that coverage is unmanageable. Then the classes can convert to computer labs, essentially, and students who are in the building can work remotely with the staff that are left. Throughout the summer and during the year, if it seems like a lot of people move between the remote plan and the building plan, it would be good to stop and think through how that would work, and call that a breakpoint.

Adapt, Respond and Overcome

The leap from old rigid websites of 2010 to the flexible ones we have now invovled lots of little steps. We still don’t have a lot of information about the way school will look in the fall, but we certainly know two ways it can look. We know what the remote learning looks like, and we can plan to make that better. We know what the building learning looks like, and we can adapt that so it is more responsive. With the two plans in hand, we can take little steps to handle whatever gets thrown our way, and in the process make our schools more adaptive and flexible.

3/9 – 20 Cases: On Tuesday morning, the day after De Blasio stated mass closures are not on the menu, I got a call from a student Michelle, who I thought was calling to thank me for finding her iPhone charger last week. She was calling because her mother has a health condition and is worried about Michelle bringing COVID-19 home. Any other day I would remind Michelle that graduation is around the corner in hopes of nudging her to push past the fear to come to school. Offering this kind of tough encouragement didn’t seem appropriate when the threat is very real. While I searched for words, I realized that I really can’t guarantee that she wouldn’t get sick at school or during her commute, and I also didn’t know how to guarantee she could finish what she needed to graduate. We finished our conversation and I began looking through my plans for the next few weeks of classes and started trying to imagine how kids could finish a multi-part project online, so I’ll be ready when other students like Melissa make the same decision.
As a teacher, I plan activities that stretch out over weeks each cycle. I’ve built big projects and planned ways students interact and collaborate as they learn. The eerily empty class I taught Tuesday, left me with stacks of unused worksheets, hollow discussions, and the question of how what could be translated to an online session for students who couldn’t be there. Unlike usual absences, I can’t assume that students are going to rejoin the class in a day or two. My whole approach to planning for their learning would change. At the same that my teaching is morphing into a dual and remote learning, there doesn’t seem to be any forgiveness in what is expected. Graduation dates, state testing dates, and the consequences our schools and our students face for underperforming haven’t changed, which adds considerable weight to any changes we are considering. If schools were to shut down, I could focus on making the most of this different model, but until then it’s like the captain of a sinking ship having to make sure every students in the water can get a life preserver while also having to bail water and keep the boat afloat for the students who are still on board.

3/11 – 44 Cases: A student was huddled around my desk arousing enough suspicion for me to jokingly ask, “Hey, what are you doing?” They turned around and I saw the student using my desk size hand sanitizer dispenser to fill up their portable container. “I ran out and nobody had any so I figured I filled up.” I wanted to be able to joke in that moment as humor is the bedrock of all of my student relationships, but I couldn’t hide the genuine concern that flashed across my face. The student stopped pumping. “My bad, but don’t worry, you have enough and I have enough.” They capped their 3/4 full container, and I replied. “Thanks. Don’t worry we just ordered more.” We laughed nervously, and I hoped that our school’s order isn’t delayed.
Perhaps the first job of schools is to provide a safe place for children and that is also difficult. Our school has been running out of supplies like hand sanitizer, and cleaning wipes, and our vendors are out of stock. The supply we need is a Coronavirus test, but those are unobtainium at this point. New York isn’t providing fast testing for the virus, so no one in the school can say they are not infected or contagious, even if they are symptom-free. De Blasio has said children aren’t “at high risk”, but children can get sick and infect their loved ones, even if they have washed their hands and sanitized their laptop. If we can’t ensure that schools won’t be places to spread the infection, then we are imposing suffocating anxiety and perhaps deadly harm for the vulnerable people who need those schools services.

3/12 – 95 Cases: On Thursday we had a student who had to go to the hospital. A typical teenage injury, that requires a member of school personnel to travel with EMS to the hospital and wait in the ER until the parents arrive. As I typically help the nurse figure out who should go, I went down the phone list to see who could help the student I kept hesitating. “They are pretty old, so is that person, and they have pre-existing conditions. What if they sit next to a person with COVID-19 who is waiting to be assessed?” As the disease spreads, the closer it gets to the school. Today’s routine trip the hospital feels like Russian roulette, and the emotional labor is palpable. Someone agreed to go, but I felt really bad about it. Their close friend is pregnant. “I’ll be fine, right?” they asked. I froze, my hesitation providing my answer. Luckily I got a text that the nurse found someone else to go. We both shared a deep sigh and exhaled most of the anxiety.
As an administrator and a teacher, I also have to support all the school staff. The emotional tension of trying to make learning happen amid all of this uncertainty is increasing in proportion with NYC’s growing number of COVID-19 cases. It is hard to have a safe learning experience when we don’t know that everyone isn’t going to get sick, or isn’t already sick. NBA player Rudy Gobert looked perfectly fine playing basketball, and showed no symptoms, despite testing positive and infecting others. Sustaining morale is a serious job, as this situation is wearing on the mental health of everyone in the school community. Lots of daily operations are now fraught with more emotional weight making the day really hard. Also making the days hard is the lack of change in what our charge is. We worked hard making to get students to graduate, and as our plans are impacted more each day, we have yet to hear calls for schools to have time for more long-term planning. The future is also lacks clarity around standardized assessment expectations, and school accountability metrics, as each day sees our goals become more and more unrealistic. If meeting the needs of the vulnerable populations is important, we need to acknowledge that meeting everyone’s needs just became much more difficult, and we need time to adjust, not a mandate to stay the course.

3/13 – 154 Cases: Friday’s staff meeting involved getting ready for an unclear future. I lead a quick session about putting information for students’ classes online and then tried to field questions. “What about students who can’t get online? Can we give them the computers from our laptop cart? Will having those laptops make them a walking target?” It was quickly clear that we didn’t have time to answer the questions around how to support learning while also having the added burden of finishing the meeting with time to prepare for class. After we broke I talked with one teacher who already had their stuff online. They were planning to use their sick days to stop coming to work because they didn’t want to risk coming in. I tried to convey that doing so is the right choice is for them, and for the larger effort of stopping the spread of the virus. Mentally, I add another name to our coverage list, including a teacher who has to pick their child up from college.
De Blasio said that schools are being kept open to provide social services for our most vulnerable students. The meals, medical services, and child care are important for a population of people who may need to continue working through any possible shutdown. The schools that we have designed to do a great job of that during the school year with a regular population. With a growing portion of the student population choosing to stay home, and with staff members as well needing to stay home as well, our schools are quickly becoming poor facsimiles of the institutions that are an important part of the social safety net. Schools do a very important job, but that isn’t the job that we can do right now because of the reality of this situation. Right now we staff have to face our own lives, which are changing dramatically outside of school. Inside school, we have to face uncertainty about whether we are safe because we don’t know about the nature of the disease, and whether our safeguards are going to be enough. We are also figuring out how to run a remote learning operation for all the students who aren’t there, while trying to adjust the learning experience for the students who are still coming.

3/15 269 Cases: I partially my name to the coverage list, as my daughter’s daycare closes for two weeks. My wife and I will have to split time between caring for our two year old, and working at our respective schools.
As I’m sitting down to think about the upcoming week, I can’t help but worry about our school’s ability to do the things the Mayor envisions. If we have to create a new educational method on the fly, while also fearing for the health of us and our loved ones, in a country facing shortages of supplies like masks and hand sanitizer, it makes sense to admit that we aren’t able to serve the role and find other ways to ensure that our most vulnerable populations get their needs met. The summer school model, or the emergency model of schools could work in the short term while teachers figure out how to best help the students who are not coming to school. For students who aren’t coming to school, let’s not demand that they come to school until we can ensure their safety, meaning having stocks of supplies and also having more testing, and faster testing available for all, not just celebrities. None of us are trained to manage an ongoing crisis. We’re here to help students learn, but going into a school where you fear for your health and the health of your loved ones and your students, isn’t a good place for learning. Let’s close the schools, and let the teachers try their hand at remote learning until we can ensure that the environment is safe enough for us to do our job.