This cycle we’re focusing on Quadratic Equations. The topic of quadratic equations has been a bit of a murky area in our transfer school. We don’t necessarily have a scope and sequence, and teach a bunch of modules, and it seemed to me we weren’t giving fair treatment to Quadratic functions. I had one project “The Function Field Guide” that covered the topic in brief details, but thought we could create a new module so kids could understand all the cool things about these functions. Creating this module has been going good so far, so I figured it would be good to blog about the broad strokes behind it’s construction and roll out.
Visual focus from the beginning
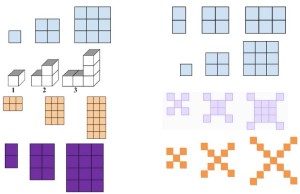
I wanted students to understand the purpose for the quadratic equations centra distinction from the function that most stduents think of when they think of equation (linear functions of the y=mx+b variety) so I started by showing this pattern. From this the students sat and thought about the pattern of growth in the table, and how they coudl represent it. on one hand we saw that it was not going up by a regular amount, that “It was going up by odds” and on the other hand some one looking at the fact that it was a square could see that the area of square would be x*x. We talked about this a lot over the first day. I thought it was too much because the kids seemed bored, but I’m not sure if the connection between the two methods was understood. THe kids seemed unsatisfied by not being able to tie their “odd” noticing to something concrete. So we kept doing visual patterns at the beginning of every class varying between quadratic and linear, and after defining the terms the kids now have an added task with each visual pattern, (is it quadratic, or is it linear, or something else?).
Fixing potholes along the way
‘Fixing the potholes’ is a term coined by the East Side Community School teachers talk of the MSRI event (around 56:00). The idea is basically to fill in pot holes on the way to new destinations, not tear up and repave roads without making any forward progress. If you find engaging problems to inspire kids to understand higher mathematics, the kids will realize what areas they need to work on. Then we tie their curiosity to the need to repair their old understandings, and provide the space for that “pothole-filling” as we pave the road into more interesting content. I much prefer this to traditional review: teaching it the same as before, but faster and with less support.
Instead of starting with an introduction on graphing, equations, linear functions I decided to work situations into the class where we do the review along the way. So when we started off looking at these patterns and classified the idea of a quadratic pattern, I get a chance to review linear functions for the students who may not have been signed up for my linear module and can benefit from seeing it in a new light.
Begin with vertex format
In the past when I’ve taught quadratics I’ve taught standard form and factored form first, because kids are often familiar with the operation of going back and forth between those two. This year I am starting with the f(x) = a(x + h)2 + k form of function because I think these are the kinds of functions kids will generate on their own when looking at visual patterns. If I see patterns like the ones above, I am not going to think, “oh, it’s like that square function, but we have to add two to it first” or “oh, it’s like that square function but with an extra thing on the side. If kids are comfortable making and using these this form, they can quickly translate it to a graph, and we can start to make sense of the graph from there.
Building tent posts with reflective writing
So my way of thinking about this unit is kind of like building this series of mathematical tent posts, like a circus tent. We get the main ones up, then all the little side posts and supports. A the end of the unit, we’ll have created a place where kids can play around or build something cool. The tent posts I’m planning will be the big thought for the week, and we’ll do it every Friday. I’ll keep these big ideas on chart paper some where in the room to keep referring to through the week. I’ll also ask kids to write about it, as well as create an example.
This tent post is pretty good so far. The first big thought was what distinguishes a linear relationship from a quadratic relationship. Last week was the shifts of the parabola and the connection to the vertex format. Next week will probably involve either a further exploration of the parabola graph, the general function of the parabola, or maybe both.
Searching for the final project
My plan is to end up with a final modeling project. I have done a few things before, but I’m hoping I can find something better. Since the last thing we will cover will involve the factored form and finding zeros as an important component. Projectile motion makes a lot of sense, but that will involve a lot of physics. I doubt I will have enough time to teach physics with understanding and I refuse to end this unit by telling kids “Here’s this function, don’t worry if you don’t understand it, just plug your numbers in.”
If you have any ideas for a good ending project, let me know in the comments!