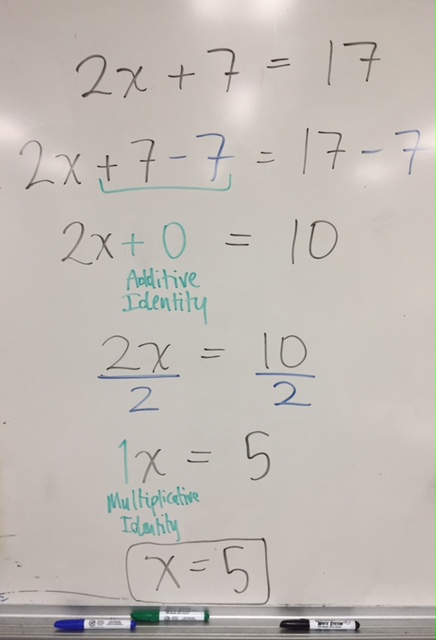Today in my Algebra 2 class we solved equations. I started with a simple worksheet – solving linear and quadratic equations with one variable. Easy stuff. But as I looked around the room I was very happy with what I saw. My students were all working diligently. More importantly they were working together. Many had left their seats to ask for help. Others were moving between groups confirming their answers. At this point in the year, I was proud to see my students motivated and working hard. I remember in my early years, as the year wound down, my students would become less and less willing to work and more and more likely to try to distract me from teaching. I suppose I’ve come a long way. Some thoughts…
My students like easy work. This is somewhat bothersome. I don’t blame them for liking what they are already able to do, but I would like to think they they would prefer a challenge, something that would lead to real thinking, new understanding and growth. I often get the feeling that they would rather just practice math that they already know. Like they just want to stay inside their comfort zone, all the way in the middle of their own personal ZPD. Today’s class was engaging, not because it was a great mathematical exploration but because it was review. This is frustrating for me.
Opportunities to build confidence are important. This is a counter to my last point. I think it’s important to embed math that my students are already good at into my lessons. For one, it’s always good to review. Secondly, it gives students opportunities to share things they know with new people. Third, and most importantly, it helps them remind themselves that there is some math they are good at. As my students worked through the problem set, I heard them saying things like, “I feel smart!” and “I get this!” That’s got to be worth something. And I think it turned their brains on for the rest of the class period. Like they got a little confidence/adrenaline boost from completing the problems. It also gave the students who typically struggle an opportunity to be on level footing with the ones who typically thrive. Definitely worthwhile.
My students have learned to work well together. This is huge. As the students worked through the problems I saw groups of students sharing answers, freshmen helping seniors, and pairs arguing about solutions and debating pathways. I see the collective effort of my class in a way that I haven’t seen in previous years. I feel great about this. It can’t be understated. It got me back to this blog!
Cancelling out is a thing for my students. Ugh. Everyone solves by cancelling out. I asked students to share how they answered the first problem: 2x + 7 = 17. Almost everyone shared that they had subtracted 7 from both sides. Okay, good. (I refrained from asking why both sides. We’ve been over this many times.) Then cancelled the 7.
Okay, how?
Huh?
How did you “cancel” the 7?
Huh? That’s just what you do.
But why does it cancel?
*Blank stares. Nobody knows.*
I think they know that 7 – 7 = 0, but I don’t think that’s part of the solving process for them. I talked about additive and multiplicative identities for a bit. I made a fuss. We moved on.
My students use procedures before thinking. After students shared the “cancelling method” I asked if anyone had done it another way. Everyone was quiet for a while so I asked Ruben. I knew he had a different method. “I just looked at it, and I knew it had to be 5,” he said. I looked at the rest of the class. “Yes?” Many of them smiled. “Well yes,” their eyes told me, “but that’s not how you do it!” I disagree. That’s how I do it! 2x + 7 = 17 ? Two times what is 10? 5. Done. They must have been taught that they shouldn’t do the problem that way. It was as if they knew they weren’t allowed. But why not!? I’m a fan of doing easy mathematics the easiest way possible. It’s efficient. If a problem doesn’t require an elaborate strategy then you should only use one if you like that sort of thing, not because you’re a robot who recognizes problem types and executes procedures. Eventually problems will get more messy and students may need a more sophisticated strategy, but until then they shouldn’t be deprived of an approach that results in the correct answer.
My students want to know why. Another huge win this year. They expect this from me. They know that I am going to talk about the whys. They knew there would be more explanation for 2x + 7 = 17, even when they already knew how to do the problem. I hope they take this with them to their next math class. I hope they demand this from themselves and their teachers. Math is not the same without the whys.
Random grouping matters. This will be another blog post. I used UNO cards this year. New seats every week. My Algebra 2 classes have students from every grade: advanced freshmen, seniors who haven’t been mathematically inclined, and everything in between. I mentioned earlier that freshmen were helping seniors. In previous years, I’d keep them separate for fear they’d make each other uncomfortable. But random grouping didn’t allow for that. The result is a classroom where more groups and pairs of students are comfortable working together. As the year has gone on I’ve become more lenient about students leaving their seat or even group to seek help and the results have been great. Again, I will post about this later. Thanks to Alex Overwijk and others at TMC15 for convincing me to do this.
I’d like to share what I did next, but that is for another post. Now, like my students, I need to stay motivated!